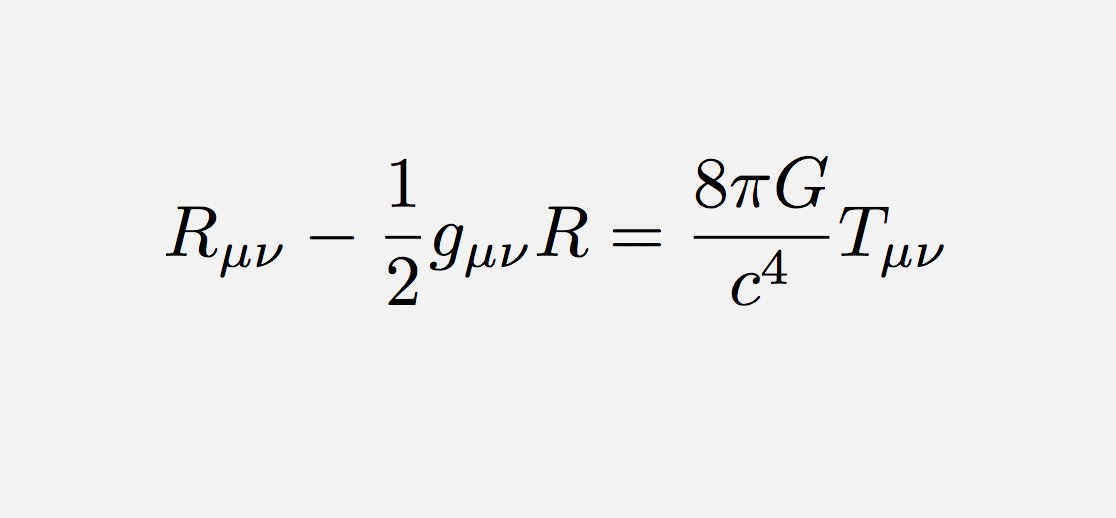Check out a recent essay I wrote on Kant's philosophy, published in Philosophy Now.
Incomplete Thoughts
Occasional and incomplete observations and reflections by Josh Mozersky
Thursday 9 June 2022
Tuesday 2 March 2021
Why Life is (Probably) Meaningless
What is the meaning of life? The short answer, there is none. There is, however, a deep reason for this answer that has to do with the conflict between how the universe operates as a whole, on the one hand, and how we naturally view reality, on the other. This leads to two questions. First, what is the nature of this conflict? Secondly, why does it exist? Once these questions are addressed, the reason for the short answer to the meaning of life becomes apparent for we shall see that life as a whole has no purpose and without purpose it does not have meaning.
Let’s begin with space and time. What the best investigation into the nature of space and time has revealed is counter-intuitive in two ways. First, it turns out that space and time are in fact aspects of a four-dimensional manifold and it is this whole that has physical significance. What this means is that its components, space on its own and time on its own, are derivate parameters and may vary so long as they add up in such a way as to preserve the properties of the whole, space-time. For example, for different observers, four-dimensional space-time will break down differently so that, between two events, more time passes for one than for the other. This is not just an effect of perspective but, rather, a mathematical consequence of how space and time jointly compose space-time, which manifests itself physically in, for example, the slowing of clocks that move at high velocities relative to the surface of the Earth, such as satellites.
Secondly, the formulas that describe space and time are simply expressions of conserved or covariant quantities that are devoid of reference to any purpose for their being what they are. They are non-intentional descriptions of natural structure. For example, in the case of four-dimensional space-time, we have Einstein’s Field Equations,
relating the distribution of matter (right-hand side) to the curvature and metrical properties of space-time (left). This is a descriptive equation and holds universally and independently of any consideration of purpose; it will not, for example, license the bending space-time specifically in order to aid or thwart our goals or plans.
Similar considerations hold with regard the equations of quantum physics, such as the Schrodinger equation,

which relates the rate of change (right-hand side) of a material system to the energy of the system (left-hand side). This holds universally and makes no exceptions on the basis of human goals or purposes; for example, the justness of a cause will not impact whether or not matter behaves in accordance with this equation.
It is important to note that the process that led to the existence of all life on the planet, i.e., evolution through natural selection, is similarly non-intentional and non-teleological. For evolution through natural selection to occur, three elements are required: variation, filtration, and replication. Variation in traits leads to differences in fitness relative to a local ecological niche, resulting in differential success in achieving reproductive maturity. If success-enhancing traits are propagated in the reproductive process, they will, over time, arise to prevalence within the population, so long as the ecological niche remains relatively stable (if not, then the organism may go extinct). Though the term can be used innocently enough, there isn’t really any selection here, just differential reproductive impact of traits given the local environment. It may appear as though a kind of creature is being fine-tuned for its surroundings, or that the two were pre-planned for each other, but nothing of the sort needs to be assumed in order to explain the rise and fall of different biological features so, accordingly, such an assumption adds nothing of scientific value to the explanation of what we observe. Variation, random or otherwise, differential reproductive success, and inheritance of traits, all occurring without an eye toward the future, will lead over time to biological adjustments better suited to the local niche. Natural selection is not, in other words, toward anything, or in the business of identifying and achieving goals.
So, nature operates non-intentionally, free of goal or purpose. Why, then, do we find it natural if not inevitable to interpret the world teleologically? Why would someone such as Aristotle find it compelling to view all of nature, including the motion of inanimate objects, in goal-oriented terms?
The answer strikes me as having to do with the pressures faced by relatively small and weak hominids in a hostile environment. Unlike a rock, which persists without the need for any input of energy, or a star, which has a large, internal store of energy, an animal’s survival depends on finding, securing, and ingesting external sources of energy. In order to persist, therefore, an animal must seek and secure resources in its niche. Animals able to do so reliably will endure; those unable to do so will perish. The required resources need not be plentiful or easy to come by, just sufficient to be attainable on a regular basis via non-fatal effort. That’s it. Life needn’t be easy, in other words, in order to persist and multiply; it can be mostly suffering and still be biologically well adapted to its environment.
So, living creatures, unlike the matter composing them, need to be goal-directed, regularly on the lookout for sources of energy, ready to pounce. It is, further, of significant help to be able to plan for the future and to anticipate; given the scarcity of resources, any skill in plotting for future success is an advantage. It is unlikely, therefore, that our ancestors would have survived for millennia in hostile environments had they taken a nonchalant or indifferent attitude toward such things as securing food, shelter, and mates. Without forming goals, human beings would lack the motivation to act in the ways required for their survival. A rock just sits there, doing nothing, unless moved by something else. The Sun just moves along its orbit burning away its nuclear energy, which it will continue to do until it is a cold, spent remnant of its former self, and it will not alter its trajectory in search of nuclear fuel; will not set off into other solar systems in order to feed itself. The Sun, in short, has no goals.
The Sun can persist for billions of years without forming goals, as can a rock. Human beings are not so lucky. If we were to simply sit still, unmoved except by external forces, then we would starve to death well before producing offspring, and the species would disappear in less than a generation. No animal can persist that lacks internal motivation, without which it will not so much as move unless rolled by an avalanche or tossed by a wave. The only way for our ancestors to survive was to seek and pursue with regularity. Accordingly, we evolved to see reality in terms of goals. We must set goals, form plans, and then act upon them.
We must, however, do more than attend to our own goals, because we are, individually, relatively weak creatures. Accordingly, we are required to work with others in order to succeed. This means we must plan and coordinate our activities with other people who are attending to their own goals and forming their own plans as a result. In short, it is essential for us to detect and pay attention to the goals of others as well as our own, for otherwise coordinated action would be unwieldy if not impossible. So, it should be no surprise that we evolved to be rather sensitive to goals and plans, whether in ourselves or others, and constantly look out for them in order to coordinate our actions. It should, further, be no surprise that we formed a tendency to overgeneralize here. Not only did our survival depend on tracking and hunting animals, who act in their own goal-oriented ways, but there was no way for the process of natural selection to know in advance where in nature goal-directed behaviour would end and mechanical behaviour would begin. It would be better to err on the side of seeing purpose where there is none rather than the reverse, for in the latter case we may become insensitive to our fellow strugglers on whose cooperation our lives depend; attributing goals and desires to rocks and stars will produce false theories but failing to work with others is often fatal.
In sum, because we want to survive and need scarce things to do so, we evolved to be oriented to reality through the lens of goals and plans, i.e., purpose. We must form and attend to our own goals and, because we are relatively weak, we must work with others to achieve our joint goals; hence, we must also be sensitive to the goals of others. Finally, since the non-intentional process of evolution cannot predict where goal-oriented activity itself will and will not evolve in the future, a bit of oversensitivity is a good bet, which means we will generalize and look for goal-like behaviour throughout nature, as did Aristotle in his physics and cosmology.
The problem, however, is that we now know from scientific investigation that nature itself is not best viewed in this way. Evolution itself is non-teleological and non-intentional, as are the physical laws that govern space-time, matter, and energy. In short, the concepts of goal and purpose only make sense from within, i.e., relative to the viewpoint of human beings; they simply do not apply to reality as a whole. While we know that human beings have goals and form purposeful behaviour as a result, the nature within which we behave has no overarching goal or purpose. It would be an instance of the fallacy of composition to assume that because entities within the world have goals, so does the world itself. In relation to living beings, there exist goals in nature; otherwise, there do not.
Is an apple food? It is for us, and some other animals, but not for a rock or the Sun. Accordingly, ‘is Food’ is not a property of the apple; rather, ‘is Food for x’ is. On its own, intrinsically, the apple is not food; the property is a relational one. Why, then, do we eat apples? Because our survival depends on calories, and they have them. But note that this is an incomplete answer. We need to add, ‘and we seek that which aids our own survival’; otherwise, we might just sit around uncaring or waiting for an apple to fall in our mouths. By comparison, as noted above, though the Sun needs hydrogen for fuel, and there is hydrogen throughout the galaxy, it will not travel from system to system in search of hydrogen when it begins to run dry. We seek what we need to survive because we want to continue living, but if we remove that desire then the apple remains a source of energy but not a kind of food. It becomes something that exists but is not part of any purpose. Purpose is relative to wants and needs, so it is internal to the human perspective. What this means is that our lives as a whole lack a goal or purpose because it is only relative to being a lifeform that goals exist. Asking for the goal or purpose of life makes no sense because ‘goal/purpose’ is defined relative to life and presupposes it. By analogy, we can ask for the angle between two lines in space but not the angle of the space itself; or, while one person may be younger than another, the pair itself is neither younger nor older than anyone.
Whether or not the foregoing evolutionary speculation is correct, it is undeniable that we see the world in terms of goals and purposes, which means our cognitive orientation is ill-fitted to understanding nature as a whole, though we can overcome this difficulty with good scientific theories. Hence, the question we ask of reality, ‘what is the purpose of all this?’, is ill-suited to be answered by it because reality has no goal or purpose. One can have a meaningful life in the sense of a life filled with goals that are pursued and fulfilled, but this does not entail that there is any purpose of, or to, the whole process itself. On the assumption that meaning entails purpose, life can have no meaning.
This answer helps explain why I write, in the title, that life probably has no meaning. My answer leaves room for doubt because it depends on taking the scientific conception of reality seriously and it is possible, if unlikely, that this picture is false. Perhaps the universe was created with a purpose by an intentional being. Perhaps we were created with a specific purpose in mind by an intentional being who inhabits a purposeless universe (e.g., the simulation hypothesis). The religious worldview is in deep tension with the scientific but not, strictly speaking, incompatible with it. While I find the scientific worldview compelling it is, like all theories within that worldview, subject to revision should evidence against it arise. I think, however, that in the absence of some kind of intentional creator or the overthrow of modern science, the question as to the purpose of life makes no sense.
Monday 15 February 2021
Politics as Fluid Dynamics
Imagine a huge balance beam with 80% of the population distributed near the middle with 10% on each edge. The great mass of voters move just slightly, between the centre-left and the centre-right. Overall the scale doesn’t move very much and, accordingly, neither side is too disturbed when the other wins an election, because nothing shifts very much from their own preferred position. So there is stability overall and each side can view the other as an opponent rather than an enemy.
To those on the fringes, the whole thing looks like a sham. They see what looks to be a single Party with two branches, each taking turns in power but neither one offering any real alternative to the other. From the edges it appears to be a rigged game in which only a thin slice of orthodoxy is tolerated. Those on the outside looking in will want deep and fundamental change at the core of the system, and will likely see advocates for either part of the mainstream as fools or dupes.
With enough time, even those in the 80% start to feel dissatisfied. Against the background of years of domestic stability, the minor differences between centrist opponents begin to look more and more significant. The small movements in the balance begin to feel like large swings. Soon, what looks to the fringes to be essential agreement within a fixed system, looks to those clustered around the middle to be a set of deep and volatile divisions. There is no longer general agreement with minor differences, which defines opposition, but instead, divisive conflict, which defines combat. Politics becomes war.
As a result, members of the 80% start to pull away from the centre. After all, who wants to be associated with an enemy? As more and more move toward the edges, the swings in the balance become increasingly extreme. This causes the “enemy” to appear increasingly dangerous because their moment in power now represents what is perceived to be a great departure from the other side. As the swings in the scale increase, so does the shift on each side toward its fringe, causing the swings to increase even more, causing the mass to move further, and so on, in a vicious cycle.
If something like this impacts a society, what responses are available?
One is that of the authoritarian: force everyone to move to a fixed point on the political scale and simply eliminate those who insist on remaining at the newly defined fringes. The evil of this is obvious.
Alternatively, a society could manufacture regular crises so that people overlook differences that would divide them in calmer settings. This is about as bad as the first suggestion and, at any rate, it is hard to see how it could be pulled off.
We could opt to just let the cycle play out: calm descends into instability which moves to crisis which results in a new consensus which leads to a period of calm which then descends into instability, etc. If the instability of this cycle could be dampened so that relatively little damage is done even at its worst, then this might be a reasonable path; history, however, suggests that the cost of political breakdown can be quite horrific before order is restored.
A fourth alternative is anarchism. We reject centralized authority and free people to organize themselves as they see fit, with the ability to move between organized groups to find the setup that best suits them. Instability is dampened by the freedom to move. We are no longer trying to make one balance beam support everyone.
One advantage of anarchism is that it seems consonant with human nature. As a general rule, nobody wants to be coerced by others. We are beings who deeply cherish our autonomy, creativity, and freedom. Imagine, for a moment, that a perfectly free and fair election leads to a government that follows proper protocol in passing a law banning all books of history. Would you feel that the government is to be obeyed on this issue, just because it was fairly elected? What if it passed a law outlawing your scientific beliefs? Clearly political authority doesn't just come for free with the political process.
Human beings are diverse and will continue to disagree about their most cherished values, including the very foundations of government itself. For some, a certain amount of coercion is acceptable. For others, no amount of coercion is tolerable. Some might be willing to ban books. Others unwilling to accept a single word of censorship. Is there a realistic hope of including all viewpoints in a single system? It is not clear that there is. Given that government is centralized coercive power, it seems inevitable that it will end up forcing large numbers of people to live lives in conflict with their deepest held values. Why not opt for a system of anarchic free association?
Thursday 28 January 2021
The Tripartite Nature of Philosophy
As a general rule, philosophy is pursued in the hope that it will provide understanding, guidance, or meaning. Let us call these the alethic, teleological, and therapeutic modes of philosophical inquiry insofar as the first is focused on truth, the second on purpose, and the third on the easing of suffering. In most philosophical schools, these three philosophical projects are considered to be thoroughly interrelated and, therefore, pursued jointly, though it is typical for the alethic to be given the central or foundational role. Plato, for instance, gives pride of place to the pursuit of truth, not only because he believes that most beliefs are generally unfounded and, at best, partial truths, but because he is convinced that once we overcome our default state of ignorance we will discover both the depths and heights of the form of the Good, which can then guide belief and action and, being eternal and immutable, offer a stable calm against the vicissitudes of life. Alternatively, we may consider the Buddhist philosophical system whose primary aim appears to be therapeutic but bases its prescriptions on profound truths about existence, such as the ubiquity of suffering. Stoic philosophy grounds its therapeutic prescriptions on a deterministic metaphysics that leaves no room for relief in anything other than mastery of one’s own thinking. Aristotle, perhaps most famously of all, derives his moral prescriptions from his observations about human nature, arguing that what we ought to do and what we will find fulfilling will follow from knowledge of what kind of creature we are. And so on.
One can certainly conceive of a discipline that puts the reduction of suffering ahead of understanding. For instance, if suffering can be alleviated by medication, then there is the possibility of finding relief in life directly rather than via the pursuit of any truth other than the truth concerning which medication eliminates which symptoms. So, there is certainly room for direct medical therapy as distinct from the indirect philosophical kind.
One can similarly imagine purpose being found in traditions that are adopted without any particular interest in prosecuting their evidential basis or truth simply because they offer a narrative context in which daily activities and life goals find a place. Hence, there is room for religious or cultural institutions to serve the pursuit of guidance and meaning in ways that are distinct from the traditionally philosophical ways of so doing.
We see, then, that what distinguishes philosophy from other pursuits that aim at purpose and peace is the commitment to grounding the latter two in the deepest possible understanding of ourselves and reality. Philosophy seeks to address the most important human problems via the pursuit of truth rather than via tradition, religion, fads, or medicine. This is not to say, of course, that addressing the problems of life in these latter ways is necessarily inappropriate or wrongheaded. It is just to say that what makes the pursuit of purpose or meaning philosophical is to approach it through the deepening of one’s understanding of the world rather than some other path.
It is, furthermore, possible that non-alethic pursuits will be of service in the philosophical journey. For instance, perhaps the experience of addressing anxiety via the ingestion of psychedelic substances will lead to new hypotheses concerning human consciousness that can be tested scientifically, thereby allowing us to come to a deeper understanding of the nature of mind. Still, what makes the pursuit philosophical is the ultimate nature of the pathway to purpose and meaning, i.e., whether the road is the road of deeper and higher quality truth or something else.
The examination of the history of philosophy leaves it all but impossible to deny any of this. From Thales to Democritus to Pythagoras to Plato to Aristotle to Aquinas to Descartes to Kant to Schopenhauer to Russell to Chomsky, the common thread is manifest: if we are to address the deepest problems of the human condition we must understand it at the deepest possible level, even if our investigations ultimately lead to the conclusion that we are incapable of such understanding, for that then is, on this skeptical view, the deepest understanding from which the truths of purpose and meaning will be derived (perhaps that there is no purpose or meaning).
This is a large part of why philosophical writing is often unnatural, fine-grained, and technical. The philosopher aims to go beyond and below ordinary thinking, so there is a real danger that standard terms and concepts will not be well-suited to the job; hence, a semi-mathematical, logical vocabulary that is stripped of the connotations of ordinary language is employed as an inoculation against importing the pre-conceptions of the superficial level of thought into the pursuit of secrets of the deep. At the same time, the opposing danger lurks as philosophers can be guilty of creating jargon that masquerades as deep thought but in fact functions as no more than an opaque repackaging of trivial ideas or the expression of meaningless nonsense. To do philosophy properly, let alone well, is no easy feat and there is no guarantee of success even after diligent, honest labor.
Another reason that philosophy is often written in semi-mathematical “logic-ese” is its long-standing and historically symbiotic partnership with natural science. 2500 years ago, Pythagoras argued that the nature of reality is mathematical, and ever since Newton natural science has progressed primarily in proportion to its mathematization. To paraphrase Galileo, mathematics is the language of nature. Nonetheless, human nature has resisted our attempts, mathematical or otherwise, at comprehensive understanding. To this day such questions as the nature of language, perception, consciousness, truth, the mind-body relation, and so on, remain about as mysterious as ever. Still, given that we are part of nature, and that non-human nature is best understood in mathematical terms, there is a perfectly understandable, even if ultimately misguided, urge to understand humanity by working out theories in terms of some kind of formal language, as seen in philosophers such as Plato, Leibniz, Frege, Russell, early Wittgenstein, Carnap, Quine, etc.
Analytic philosophy is often accused of “logic chopping” i.e., of focusing on minute semantic or syntactic distinctions that are divorced from any larger concerns such as purpose or meaning. It is understandable why one who is accustomed to the grander, narrative style of a Nietzsche, Heidegger, Foucault, or Rorty would feel this way. And, while it is certainly true that some analytic philosophy pursues question of no serious significance, I do not think the larger complaint is on target, for the reasons just outlined. Philosophy, whatever it is, is the alethic route to purpose and meaning and if one wants deep purpose and meaning then it is natural to want deep investigation into the nature of reality. Hence, the search for the right language, the right framework, and the right tools, are all of genuine importance. It is not a surprise, then, that philosophy since the beginning of the 20th Century has ended up significantly preoccupied with questions such the nature of language and logic, even if it goes overboard at times.
Should philosophy, especially of the analytic variety, be more focused on issues of meaning and purpose? Perhaps, but it is not as if such questions haven’t been pursued by analytic philosophers such as Bertrand Russell, Adolph Grünbaum, Nicholas Rescher, Noam Chomsky, Daniel Dennett, Thomas Nagel, David Lewis, John Leslie, Shelly Kagan, Samuel Scheffler David Benatar, etc., etc. The questions are asked, answers proposed, objections considered, and the logic of the language used put under scrutiny. It may not be to everyone’s taste, but it is certainly squarely in the 2500-year tradition of philosophy.
Monday 25 January 2021
COVID-19, Probability, Risk
In a recent article in Scientific American, authors Nathan Ballantyne, Jared Celniker, and Peter Ditto examine the question as to whether images of the impact of COVID-19, such as ill people in hospital beds, can help bypass the “persuasion fatigue” that is setting in as people tire of arguing over whether the disease is sufficiently serious to justify the series of lockdowns and other restrictions imposed by governments around the world. If sharing arguments and statistics hasn’t settled the issue to date, then perhaps graphic photographic evidence will do the trick by shocking doubters into agreement with those who preach the seriousness of the disease and the appropriateness of government action.
As the authors point out, the efficacy of even explicit photographs is minimal. The problem, they argue, is that photographs have a powerful emotional impact, such as shock or disgust, primarily for those already convinced of the terrible nature of the situation represented in the picture. If, on the other hand, “you entered our study doubting the threat, the images didn’t shock you and, accordingly, didn’t move your thinking… one person’s shock is another person’s shrug”, write the authors.
The limitation of photographic evidence to persuade, they conclude is a result of an “empathy gap” whereby we mistakenly assume that what moves us is what moves others, and in similar ways. This is a kind of emotional question-begging, whereby “when using images to persuade, we may take for granted precisely what we’re trying to prove” (italics in original).
I think this is all basically correct, but I think that the failure of “empathy” in these cases is in fact a disagreement over risk.
To see this consider the economic concept of expected value. When considering whether to undertake some action, A, one generally considers two factors: first, what is likely to happen should A be undertaken; secondly, what is the impact of those possible happenings. For example, in deliberating whether or not to attend law school, one may try to estimate the probability of getting a legal job upon completion with all the benefits that entails, such as easily paying off student loans. This will be balanced against the probability of not getting such a job and having to pay off student loans in those circumstances. This combination – probability (legal job) x benefit (legal job) + probability (no legal job) x cost (no legal job) – is the expected value of the decision to attend law school.
Notice that even if the cost of failing to secure a legal job is very high – suppose the student loans will take a lifetime to pay off in that case – one may reasonably decide to ignore that outcome if the probability of it happening is sufficiently low. If, for example, there is a 99.9% chance of getting a job as a lawyer upon completion of the law degree, then it may make perfect sense to take on very large student loans to complete the degree assuming a lawyer’s salary is high enough. If, on the other hand, the salary of a lawyer is not very high, then it may make no sense to pursue a law degree even if there is a 100% chance of getting a job at the end. Similarly, if one considers an outcome to be sufficiently bad, then even a very low probability of occurrence might be compelling; for example, one may refuse to skydive because one takes the very low probability of death to outweigh the enjoyment of the very high probability safe landing. What matters, in other words, is not just the goodness or badness of the outcome but its probability of occurrence, and a decision can only be assessed if both dimensions are taken into account.
Consider, for example, something very familiar: getting in a car and driving to work. We all know that a serious car accident, such as a highway collision, is a very bad outcome: death or serious injury usually result. Still, one will likely be willing to get on the highway and drive to work every day so long as the probability of such a bad outcome is sufficiently low, which in fact it is. In such a case, one will take the chance knowing how bad the outcome is. Even if one is shown a gruesome image of the aftermath of a highway collision, then one will likely continue to drive to work because the image addresses the cost of an accident not its probability. This is a general feature of a photograph: because it shows a single incident, it cannot tell us very much at all about the probability of such an incident occurring. Similarly, an image of a victim of a violent mugging in another city will not cause one to stay home at night unless one is convinced that such a beating is sufficiently likely to occur to oneself when out on the street. If not, then the picture will have minimal impact.
Something important should be made explicit, however: there is a subjective element to all of this, namely, at what probability does a bad outcome become too risky? There is no agreed upon answer to this. We each have our own set of risk tolerances.
So, the logic of the “empathy gap” is in fact a disagreement over what counts as a reasonable risk. Some believe that COVID-19 poses a probability of suffering or death sufficiently low to be worth risking exposure. For them, images of such suffering or death simply miss the point: they may make vivid how badly things may go but not how likely it is that they will go that way. These are like people who continue to drive to work knowing that there is a chance they die in the process. For those, on the other hand, sufficiently moved by the badness of the disease to think that even a very low probability of death or suffering is not worth the risk, then a graphic image will just reinforce what they already believe: that the disease is too horrible to take a chance on. They are like people who refuse to skydive despite the safety record or parachutes.
In other words, for one side, the low probability outweighs the magnitude of the outcome while, for the other, the magnitude of the outcome outweighs the low probability. Showing a photograph is not so much a matter of taking for granted what one is trying to prove – “the outcome of COVID-19 is horrible” – as it is an irrelevant gesture in this debate. Since a photograph doesn’t tell one how probable what it depicts is, it cannot address those who think the risk is low enough to be worth taking.
What of those who think the disease is no worse than the flu or who think it is a hoax? The former would be those who dispute the consensus of the medical community: how likely are they to see one or two photographs as convincing? The latter are those who dismiss the evidence and opinions of the medical community as bogus: how likely are they to see some photographs as veridical, rather than fakes? In both cases we have a similar problem of assessing probabilities. The first group, for whatever reason, considers the medical evidence to date to give a low probability to the proposition that COVID-19 is much worse than the flu, so is likely to see a few bad photographed cases as outliers, the kind of thing that happens in any flu season. The second group assigns no significant probability to anything the medical community has to say on the matter, so will assign a higher probability to the photograph being a fake than anything else. In short, for those who have lost trust in the medical establishment, some gruesome pictures will be dismissed as irrelevant or fakes. For those who have not lost their trust, a photograph cannot tell them the probability of what is depicted therein, so cannot impact their assessment of the risk involved in locking down or not.
We see, then, why there is no way to close an empathy gap with any photographic intervention: the problem is a logical one of probability plus outcome underdetermining risk tolerance, which is subjective. Photographs simply don't address that issue.
Thursday 27 August 2020
Scientific Theory and Lived Experience
In 1927, astronomer George Lemaître published a paper which pointed out that, when applied to the universe as a whole, Einstein’s General Relativistic field equations have no static solutions: either the universe is expanding or else it is collapsing (Lemaître 1927). Einstein himself found this conclusion unsatisfactory, so he modified his equations to include a term – the ‘cosmological constant’ – that would counter-balance any potential expansion or contraction, thereby producing a model of a fixed universe with no beginning or end (Einstein 1931). In 1929, the astronomer Edwin Hubble presented observations confirming that the universe is indeed expanding (Hubble 1929), as predicted by the original equations of General Relativity, leading Einstein to eventually call the cosmological constant his 'biggest blunder.' Had Einstein, instead, trusted and followed his equations, he could have been the first to predict the expansion of the universe and, by running things backward, the Big Bang itself. (Note: currently, the effect of dark matter on the universe is thought, by some, to be well accounted for by the reintroduction of the cosmological constant, though not to counter-balance expansion but to accelerate it; so the expansionary implications of General Relativity would still have been rightly predicted by Einstein had he stuck to his equations).
Einstein also resisted another implication of his theory: that a sufficiently massive body would collapse to a point of infinite density creating a bottomless well in spacetime from which nothing could escape, now commonly known as a black hole. Einstein disliked the idea, which represented a discontinuity in the fabric of spacetime, so he worked to discover some mechanism that would de facto prevent matter from collapsing to such a point:
The “Schwarzschild singularity” [i.e. black hole] does not appear for the reason that matter cannot be concentrated arbitrarily. And this is due to the fact that otherwise the constituting particles would reach the velocity of light. (Einstein 1939, p. 936)
In other words, a black hole is impossible because it would require matter to violate an ironclad implication of Special Relativity: nothing can accelerate to the speed of light. This, however, turns out to be untrue (i.e. it does not require such acceleration), and today black holes are regularly detected by astronomers. Once again, Einstein would have been well advised to have trusted his equations.
A similar conflict between mathematics and physical intuition befalls anyone who attempts to understand quantum mechanics, which entails that physical systems are regularly in a state of superposition. Superposition is almost impossible to interpret physically because it represents a system as being distributed between discrete states; e.g. a particle is both in position p1 and position p2. All the same, superposition is mathematically straightforward and can be used to make extremely precise predictions. As it turns out, quantum mechanics is generally regarded as the most predictively successful theory of all time (Lewis 2016). Accordingly, if we follow the math, even without understanding its physical significance, then we can predict which states of a physical system will be observed and when.
These cases are illustrative. When even a great thinker’s philosophical or commonsensical beliefs conflict with counterintuitive laws of nature (mathematically described), the latter often emerge victorious and have done so on historically significant occasions. There is no reason to doubt that Einstein’s commitments to both a steady-state and continuous universe were sincere and grounded in serious reflection. Still, he was wrong; here are examples in which the greatest scientist in human history, reflecting on his own greatest achievement, was led astray by his philosophical commitments about the nature of reality as a whole. All of this is a bit surprising. After all, it was Einstein who, correctly, insisted that we reject what experience tells us about the nature of space, time, and motion in favour of his Relativistic equations.
In classical phenomenology, stemming from Husserl, ‘lived experience’ is experience as one finds it. Attending to lived experience, then, is paying attention to one’s experiences as they are, without the influence of interpretation or theory. But, of course, it is everyone’s lived experience that time and space are absolute (the same for everyone everywhere), immutable (unaffected by matter or events), and distinct (one can move back and forth in space but not time). Nevertheless, Einstein's theories entail that space and time vary by frame of reference, are altered by matter and gravity, and are mathematically connected components of a four-dimensional whole. Einstein’s conclusions have been empirically confirmed. For example, if one were to construct a GPS system without employing his equations, one would be left with unusable devices – one needs to account for the ways in which space and time vary with speed and gravity in order to pinpoint a precise location on a map using trilateration from known satellite positions. Importantly, this does not change the experience of space and time. Spacetime impacts us psychologically just as it did prior to Einstein, seeming to split into two distinct, unchanging, and universal measures. All the same, we now know this experience to be a poor guide to the nature of space and time themselves.
If one takes a look up at the darkened sky, night after night, what one sees is effectively unchanged; there is certainly no experience of space itself expanding. But experience is a poor guide here; space is not only expanding in all directions but is accelerating outward, as noted above. Even Einstein was misled.
In a post-Darwinian world, it should not surprise us that there might exist some conflict between common sense, philosophical commitments, or lived experience, on the one hand, and the laws of nature, on the other. We now know that human beings are the products of nature: we have evolved through a process of variation, selection, and inheritance that favours traits that contribute to the production of offspring that survive to reproductive maturity. This is how we came to be what we are. It is entirely possible, accordingly, that certain cognitive shortcuts have been favored by evolution because they help, or at least fail to hinder, reproductive success by conferring advantages, such as energy efficiency or simplicity, if not accuracy. These shortcuts could, for example, lead us to find it instinctive to view the world a certain way – there is an evolutionary advantage, or lack of harm, in doing so – even though this way of seeing things obscures certain details, or applies in only local or special cases. We should not, in other words, presume that natural cognitive strategies will be fully generalizable because they developed as solutions to local problems.
What is surprising is that we are, somehow, able to learn some fully generalizable laws. We could very well have evolved without any capacity to know the large-scale features of reality, just as other creatures – fish, bears, beetles – have in fact done. We somehow managed the trick, however, and we can be confident in this because of the surprising predictive successes of theories such as Einstein’s General Relativity and quantum mechanics. We would have little reason to suppose that human reason could extend beyond the local conditions under which it evolved were it not for cases such as these where mathematical formalism, often not easily interpreted, leads to surprising predictions that are confirmed, repeatedly and to high degrees of precision. Somehow, the mind is able to construct models that apply everywhere and every-when, even though the brain itself evolved under spatiotemporally limited pressures. While we don’t know how this happened, we can hazard some guesses. For example, whichever features of the universe are truly universal will thereby hold in any local conditions under which human beings faced evolutionary challenges and may leave their mark there. Hence, a sufficiently sophisticated cognitive organ, forged by evolutionary forces in a local environment, could pick up the scent of the universal; human brains might have evolved a mechanism for detecting subtle but available imprints of large-scale structure that, when combined with the ability to generalize and extrapolate, allow us to posit universal laws that can be tested observationally. We currently do not know the actual story, but something like this is clearly possible, for we regularly predict with success, at least in the natural sciences.
All the same, that our evolved heuristics might have built-in blind spots with regard to the large-scale structure of reality is not surprising; perhaps it is to be expected. We should not, however, lose sight of the fact that such blind spots might equally well exist with regard to the inner world of thought and experience. The brain, like other evolved organs, has its limits, and our knowledge of any part of the world is dependent on its scope, power, and resolution. There is little reason to suppose that the scope is limitless, the power infinite, the resolution perfect. Much as the eye is not naturally able to see itself, or the tongue to taste itself, it may be that the brain is not well-evolved to know itself. Various aspects of the inner workings of our own cognitive system may, in other words, be as hidden or counterintuitive as the outer workings of spacetime; the brain is, after all, a natural system too. What is delivered to the mind by reflection on our own cognition and experiences may mislead, just as happened to Einstein when he reflected on his experience of the universe as a whole. The brain, being a physical system, may have structural features that escape what the it itself evolved to deliver to reflection, which historically needed to be focused on what is most essential for survival and reproduction. It may, of course, be possible to overcome some cognitive limitations by pooling resources (linking brains together), inventing new instruments of investigation (MRIs), and the careful use of experiment, observation, and analysis; we can, by comparison, use tools such as mirrors to allow they eye to see itself. But there is no particularly good reason to suppose that the immediate, unreflective impressions delivered by a mind about itself should have some unrevisable character, especially when up against well confirmed scientific models. Perhaps thinking about thinking is infallible; perhaps the experience of experience is incorrigible; but, then again, perhaps not. Maybe, when reflecting on itself, the mind relies on evolved heuristics that are subject to biases similar to those that impact the reflection on our experience of space, time, and motion. Without evidence for the infallibility or incorrigibility of the cognitive organ's operations on itself there is no way to know that lived experience is reliably informative, even about experience.
If this weren’t true, i.e. if our minds were completely and invariably self-transparent, then there would hardly be any need for the various disciplines – psychology, psychiatry, social work, etc. – that constitute modern psychotherapy. We know, however, that many, if not all, of us sometimes require the assistance of a trained outsider to truly understand what is going on within. Even if some aspects of self-reflection are infallible, it is clear from the legitimate need for psychotherapeutic professionals that not all of it is. The deeply held deliverances of reflection on inner experience are not guaranteed to be correct. Lived experience may very well matter, and deserve to be attended to, but it hardly amounts to a trump card against amassed scientific evidence.
There is more to say, of course, but I will come back to further issues in another post.
References
Einstein, A.: 1931, ‘Zum kosmologischen Problem der allgemeinen Relativitätstheorie’,
Sitzungsberichte der Preussischen Akademie der Wissenschaften, Physikalisch-mathematische Klasse, pp. 235–237
Einstein, A.: 1939, ‘On a Stationary System With Spherical Symmetry Consisting of Many Gravitating Masses’, Annals of Mathematics, Second Series, 40: pp. 922-936
Hubble, E.: 1929, ‘A Relation between Distance and Radial Velocity among Extra-Galactic Nebulae’. Proc. Nat. Acad. Sci. 15: pp. 168-73
Lemaître, G.: 1927, Discussion sur l'évolution de l'univers
Lewis, P. J.: 2016, Quantum Ontology: A Guide to the Metaphysics of Quantum Mechanics, Oxford University Press.